Introduction
Worked exercise
Introduction
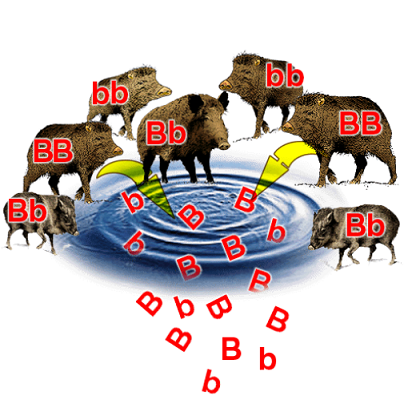
In the wild, each species may exist as one population or multiple populations. Different populations correspond to defined areas – habitats.
The sum of all present alleles for a given gene in a given population is known as the gene pool.
This is essentially a way of thinking about all the individuals in a population contributing their alleles towards the overall allele frequency.

How could we keep track of the frequency of each allele for a given trait when we have a dominant-recessive interaction? More specifically, how could we account for the visible dominant traits as homozygous or heterozygous, since both look the same?
This is where the Hardy-Weinberg principle comes in. Firstly, there are criteria for when this principle may be applied to a population:
Random mating must take place.
No migration must occur either inwards or outwards of the population.
No mutations must arise in the population.
No natural selection must take place due to one trait being better or worse adapted to the environment.
It’s apparent that this is simply rarely, if ever, the case in a real wild population. However, the Hardy-Weinberg principle is useful at predicting allele frequencies in a reliable mathematical model.
The frequency of the dominant allele is noted p while that of the recessive allele is noted q. Both must necessarily account for the whole population, therefore:
p + q = 1
The values are frequencies, so they are noted as percentages. 1 is 100% while 0.5 is 50% and 0.05 is 5%, etc.
Worked exercise
If we know that the frequency of the allele for dark fur in a population of koala bears is 0.2, and this all